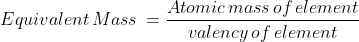This is a fundamental skill in chemistry, as you might have noticed from the short reading in stoichiometry! Balancing equations means writing chemical equations such that the amount of stuff you start with in the reaction equals the amount of stuff you end up with as a product. In other words, if I start baking bread with 10 pounds of flour, I should end up with 10 pounds of bread, unless some is lost onto the floor or if some of it goes up in smoke!
A simple example goes a long way. We can form water by combing hydrogen gas (H2) and oxygen (O2) in the presence of electricity. The reaction looks like this:
H2 + O2 ---> H2O
If you do some of the gram molecular weight calculations you will find this:
2 grams of hydrogen + 32 grams of oxygen = 18 grams of water
What this says is that you start with 34 grams of stuff and end up with 18 grams of stuff. You've lost 16 grams of stuff, and in this reaction that just doesn't happen! Where did the 16 grams go?
They're not lost, we just haven't balanced the equation! You might have also noticed that there are two oxygen s on the left and only one on the right! We need to get things in the correct proportions for this reaction to be balanced. The balanced reaction looks like this:
2 H2 + O2 ---> 2 H2O
This says that we need two hydrogen molecules to combine with one oxygen molecule to form two new water molecules. If we do the math:
(2 x 2 grams of hydrogen) + 32 grams of oxygen = (2 x 18 grams of water)
we now have 36 grams of stuff on the left and 36 grams on the right. We also now have 4 hydrogens on the left, four hydrogens on the right, two oxygens on the left, and two oxygens on the right. We can say that this equation is mass balanced. In your studies of chemistry, you will also need to be concerned with charge balancing, but we'll let your profs help you with that!
Balancing equations is an art, but if you have a calculator that can handle what is known as a "matrix", you have a foolproof way of balancing equations! A matrix is a group of numbers, arranged in rows and columns, like this:
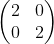
This is called a "2 by 2" or "2 x 2" matrix, because it has two rows (going across) and two columns (going down). In this application, you will have to do three matrix operations:
1. Multiply two matrices
2. Find the determinant of a matrix
3. Find the inverse of a matrix
Fortunately, graphing calculators make this particularly easy! To help you understand a little of what you are doing, let's explain finding the determinant. The determinant is a single number generated by cross-multiplying the terms in the matrix. You must have a square matrix (n X n) to be able to find the determinant. The equation for finding the determinant is:
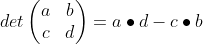
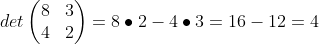
The example below the equation shows a sample calculation for a 2 x 2 matrix. Notice that you are cross multiplying the opposite terms, then subtracting out the other set of opposite set of multiplied terms. Pretty easy.
Here is how this is done on the TI-82 Graphical Calculator. These instructions are SPECIFIC to the TI-82:
1. Turn the calculator on (yep, common sense, but want to make sure that's done!)
2. Hit the "MATRIX" button
3. Use right arrow key to scroll over to "EDIT"
4. Type "1" for Matrix A
5. Type "2" for number of rows, the ENTER
6. Type "2" for number of columns, then ENTER
7. Type each of the numbers, following each with ENTER: 8-ENTER-3-ENTER-4-ENTER-2-ENTER
8. Type the blue "2nd" button then "QUIT" (above the MODE button)
9. Type MATRIX, then scroll to MATH
10. Hit "1" for "det"
11. Hit MATRIX then "1". You should see "det [A]" in the window.
12. Hit the ENTER key, you should see the result "4"
Now we are ready to talk about balancing equations. Let's choose a simple reaction:
a Cr + b O2 ---> c Cr2O3
We have two different elements, Cr and O, so we will need two different equations. We are trying to calculate the values of a, b, and c, the coefficients of the reaction. The two equations look like this:
Cr: 1a + 0b = 2c
O: 0a + 2b = 3 c
The "1a" means that there is one Cr behind the "a" coefficient, zero Cr's behind the "b" coefficient, and 2 Cr's behind the c coefficient. We use the same technique for oxygen. We now have two matrices (called Matrix A and Matrix B):
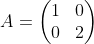
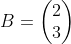
To obtain the values of a, b, and c, do these steps:
* To calculate a and b, multiply the inverse of Matrix A times Matrix B times the determinant of Matrix A: [A]-1 x [B] x det[A]
* To calculate c, calculate the determinant of Matrix A.
Here is how to do the first step:
1. Enter Matrix A as a 2x2 matrix, using the technique described above
2. Enter Matrix B as a 2x1 matrix, using the same technique
3. Once this is done, you can hit "2nd" then "QUIT" to get a blank screen.
4. Call up Matrix A by typing MATRIX 1 (you should see [A])
5. Hit "x-1" to set up the inverse
6. Hit the "x" for multiply.
7. Hit MATRIX 2 to call up Matrix B
8. Hit the "x" for multiply
9. Hit MATRIX, scroll to MATH, then 1 to do a determinant
10. Hit MATRIX 1 to call up Matrix A. You should now have: [A]-1 * [B] *det [A]
11. Hit the ENTER key to get your result of [[ 4 ] [3 ] ]. The coefficient a is equal to 4, and the coefficent b is equal to 3!
To do the second part, calculating c:
1. Hit MATRIX, scroll to MATH, select 1 for the determinant
2. Hit MATRIX 1 to call up Matrix A, hit the ENTER key to get the result for c as 2
The balanced equation is now:
4 Cr + 3 O2 ---> 2 Cr2O3
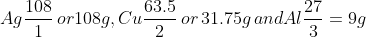 which are the equivalent masses of
which are the equivalent masses of